[프로그래머스_1] 소수 찾기 JAVA

프로그래머스

 

CODE(기본)

class Solution {
    public int solution(int n) {
        int answer = 0;
        
        boolean flag = true;
        for(int i = 2; i <= n; i++) {
            flag = true;
            if(i != 2 && i % 2 == 0) continue;
            for(int j = 2; j <= Math.sqrt(i); j++) {
                if(i % j == 0) {
                    flag = false;
                    break;
                }
            }
            
            if(flag) answer++;
        }
        return answer;
    }
}

2 ~ i의 제곱근까지 반복하며, 나누어 떨어지면 소수가 아니다. 쉽게 생각할 수 있는 i는 3, i+=2 조건으로 반복문을 돌리면 시간초과가 나며 통과가 되지 않는다.

 

CODE(에라토스테네스의 체)

class Solution {
    public int solution(int n) {
        int answer = 0;
        boolean[] check = new boolean[n+1];
        check[0] = check[1] = false;
        
        for(int i=2; i<=n; i++) check[i] = true;
        
        for(int i=2; i<=Math.sqrt(n); i++) {
            if(!check[i]) continue;
            for(int j = i; i*j<=n; j++) check[i*j] = false;
        }
        
        for(int i=2; i<=n; i++) {
            if(check[i]) answer++;
        }
        return answer;
    }
}

에라토스테네스의 체?

간단하게 설명하자면 i = 2부터 그의 제곱근까지 반복문을 돌면서 자기 자신을 제외한 i의 배수를 지워나가며, 마지막에 값이 true인 배열의 요소 개수를 return하면 소수의 개수를 찾을 수 있다.

 

 

실행 결과

좌 - 기본 / 우 - 에라토스테네스의 체

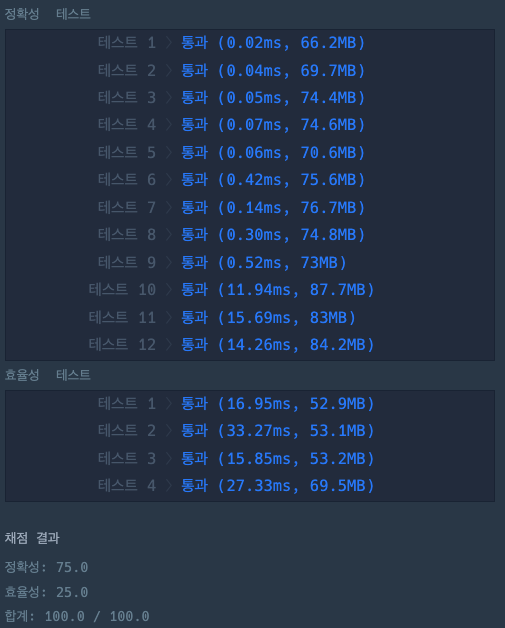
에라토스테네스의 체의 속도가 훨씬 빠른 걸 볼 수 있다.